物体のエッジを抽出するプログラムを作りたいが、どのように作ればよいか分からない。エッジ抽出の原理について詳しく知りたい。
そんな悩みを解消すべく本記事では、ノイズを除去しつつエッジ抽出するソーベルフィルタについて解説します。
まず、エッジ抽出原理を解説します。次にソーベルフィルタとは何かについての解説です。最後にPython,OpenCVを用いて画像のエッジを抽出するプログラムを解説します。
それでは始めましょう!
この記事はこんな人におすすめ!
- 画像処理を学んでいる初心者
- エッジ抽出の技術を理解したい人
- プログラミングで画像処理を実践したい人
エッジ抽出の原理
ソーベルフィルタについて理解するためには、エッジ抽出の原理を学ぶ必要があります。ここでは、微分によってエッジ検出する原理を解説します。
微分で勾配を数値化
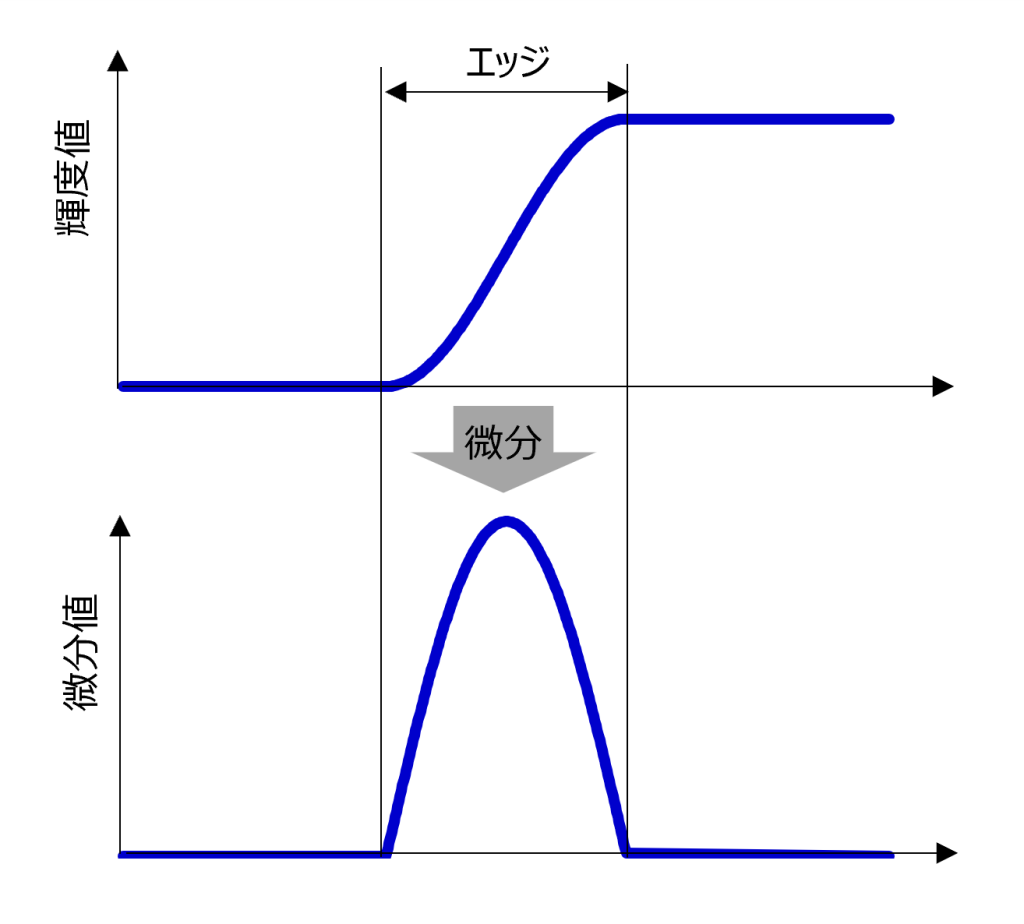
画像処理でのエッジとは、画像の明るい部分と暗い部分が急激に変化する勾配部です。この勾配部を抽出するには、画像の輝度値を微分し数値化します。関数\(f(x)\)の微分\(f'(x)\)は以下式で表されますよね。
$$f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$
下図のように、輝度値を微分した値が大きい部分がエッジに相当することが分かります。

デジタル画像は2変数かつ1画素ごとの値のため、どうやったら勾配を求められる?
偏微分
2変数関数の場合は、微分する変数を1つ指定し、それ以外の変数を定数として微分します。このような微分を偏微分といいます。2変数関数を\(f(x,y)\)とし、xで微分した導関数を\(f_x(x,y)\)、yで微分した導関数を\(f_y(x,y)\)とすると
$$f_x(x,y) = \lim_{h \to 0}\frac{f(x+h, y)-f(x, y)}{h}$$
$$f_y(x,y) = \lim_{h \to 0}\frac{f(x, y+h)-f(x, y)}{h}$$
\(f_x(x,y)\)はx方向、\(f_y(x,y)\)はy方向の勾配を表します。
微分の離散化
デジタル画像は、1画素ごとの離散値です。そのため、\(h\)は有限です。そこで、\(h=1\)として微分値を求めます。
$$f_x(x,y) = f(x+1, y)-f(x, y)$$
$$f_y(x,y) = f(x, y+1)-f(x, y)$$
これは座標\((x,y)\)とその前方座標\((x+1,y)、(x,y+1)\)の差分をとっていますので前方差分と呼ばれます。
一方、\(h=-1\)の場合は
$$f_x(x,y) = f(x, y)-f(x-1, y)$$
$$f_y(x,y) = f(x, y)-f(x, y-1)$$
となり、座標\((x,y)\)とその前方座標\((x-1,y)\)、\((x,y-1)\)の差分をとることから後方差分と呼ばれます。
また、前方差分と後方差分の平均を求めると
$$f_x(x,y) = \frac{f(x+1, y)-f(x-1, y)}{2}$$
$$f_y(x,y) = \frac{f(x, y+1)-f(x, y-1)}{2}$$
となります。座標\((x+1,y)\)と座標\((x-1,y)\)の差分、座標\((x,y+1)\)と座標\((x,y-1)\)の差分をとることから中心差分と呼ばれます。
微分フィルタ
空間フィルタリングにおいて線形フィルタは、入力画像を\(f(i,j)\)、出力画像を\(g(i,j)\)、フィルタ係数を\(h(m,n)\)とするとき、以下式で表されました。
$$g(i,j)=\sum_{n=-W}^{W}\sum_{m=-W}^{W}f(i+m,j+n)h(m,n)$$

微分をこの形式で表すと微分フィルタは以下表となります。
| x方向 | y方向 | |
| 前方差分 | \begin{pmatrix} 0 & 0 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & 0 \end{pmatrix} | \begin{pmatrix} 0 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 1 & 0 \end{pmatrix} |
| 後方差分 | \begin{pmatrix} 0 & 0 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix} | \begin{pmatrix} 0 & -1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix} |
| 中心差分 | \begin{pmatrix} 0 & 0 & 0 \\ -1/2 & 0 & 1/2 \\ 0 & 0 & 0 \end{pmatrix} | \begin{pmatrix} 0 & -1/2 & 0 \\ 0 & 0 & 0 \\ 0 & 1/2 & 0 \end{pmatrix} |
ソーベルフィルタとは
画像にノイズが混入していると、ノイズをエッジと誤検出してしまいます。
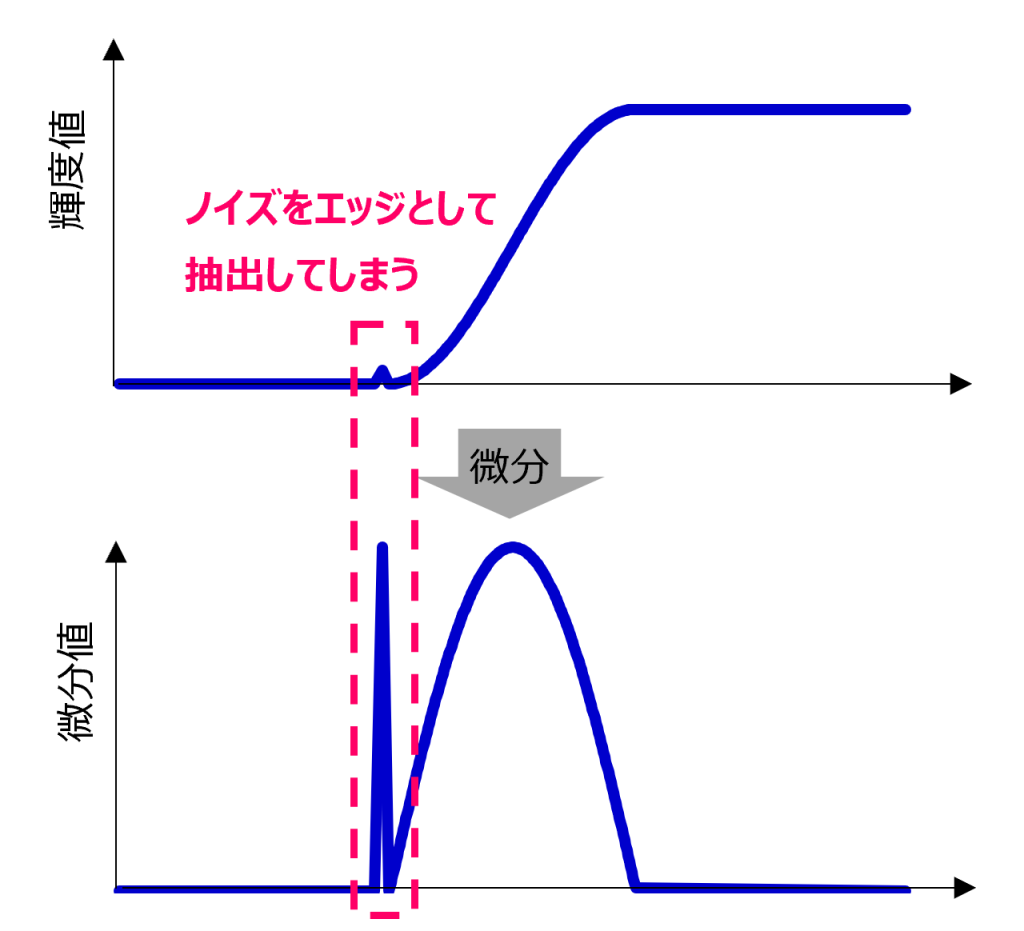
そこで登場するのが、ノイズを除去しつつエッジ抽出するソーベルフィルタです。
そこで登場するのがソーベルフィルタです。ソーベルフィルタとは、前節で説明した中央差分したのち、中央に重み付けした平滑化を行ったフィルタです。
フィルタ係数
下記表は、x方向、y方向の中央差分、重み付き平滑化、ソーベルフィルタのフィルタ係数です。
| 中央差分: \(h_1(x,y)\) | 重み付き平滑化: \(h_2(x,y)\) | ソーベルフィルタ: \(h_2(x,y)\cdot h_1(x,y)\) | |
| x方向 | \(\begin{pmatrix} 0 & 0 & 0 \\ -\frac{1}{2} & 0 & \frac{1}{2} \\ 0 & 0 & 0 \end{pmatrix}\) | \(\begin{pmatrix} 0 & \frac{1}{4} & 0 \\ 0 & \frac{2}{4} & 0 \\ 0 & \frac{1}{4} & 0 \end{pmatrix}\) | \(\frac{1}{8}\begin{pmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{pmatrix}\) |
| y方向 | \(\begin{pmatrix} 0 & -\frac{1}{2} & 0 \\ 0 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \end{pmatrix}\) | \(\begin{pmatrix} 0 & 0 & 0 \\ \frac{1}{4} & \frac{2}{4} & \frac{1}{4} \\ 0 & 0 & 0 \end{pmatrix}\) | \(\frac{1}{8}\begin{pmatrix} -1 & -2 & 1 \\ 0 & 0 & 0 \\ -1 & 2 & 1 \end{pmatrix}\) |
中央差分を\(h_1(x,y)\)、重み付き平滑化を\(h_2(x,y)\)とするとき、中央差分と重み付き平滑化を順に施したソーベルフィルタは、\(h_2(x,y)\cdot h_1(x,y)\)で計算できます。
ブリューウィットフィルタとの違い
ソーベルフィルタと同様なフィルタにブリューウィットフィルタ(Prewitt filter)というものがありますので紹介しておきます。
| 中央差分: \(h_1(x,y)\) | 平滑化: \(h_2(x,y)\) | ブリューウィットフィルタ: \(h_2(x,y)\cdot h_1(x,y)\) | |
| x方向 | \(\begin{pmatrix} 0 & 0 & 0 \\ -\frac{1}{2} & 0 & \frac{1}{2} \\ 0 & 0 & 0 \end{pmatrix}\) | \(\begin{pmatrix} 0 & \frac{1}{3} & 0 \\ 0 & \frac{1}{3} & 0 \\ 0 & \frac{1}{3} & 0 \end{pmatrix}\) | \(\frac{1}{6}\begin{pmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{pmatrix}\) |
| y方向 | \(\begin{pmatrix} 0 & -\frac{1}{2} & 0 \\ 0 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \end{pmatrix}\) | \(\begin{pmatrix} 0 & 0 & 0 \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ 0 & 0 & 0 \end{pmatrix}\) | \(\frac{1}{6}\begin{pmatrix} -1 & -1 & 1 \\ 0 & 0 & 0 \\ -1 & 1 & 1 \end{pmatrix}\) |
こちらは中央差分と重みなしの平滑化を順に施したフィルタです。
OpenCVを用いたエッジ抽出
では、PythonとOpenCVを用いて画像のエッジを抽出してみましょう。
サンプルプログラム
下記は、画像を読み込み、ソーベルフィルタを適用したサンプルプログラムです。
import cv2 as cv
def concat_tile(im_list_2d):
return cv.vconcat([cv.hconcat(im_list_h) for im_list_h in im_list_2d])
img = cv.imread("sample.jpg") # 写真の読み込み
img_sobelx = cv.Sobel(img, cv.CV_64F, 1, 0, ksize=3) # 3x3の横方向ソーベルフィルタ
img_sobelx = cv.convertScaleAbs(img_sobelx)
img_sobely = cv.Sobel(img, cv.CV_64F, 0, 1, ksize=3) # 3x3の縦方向ソーベルフィルタ
img_sobely = cv.convertScaleAbs(img_sobely)
img_gradient = cv.addWeighted(img_sobelx, 0.5, img_sobely, 0.5, 0) # 勾配の大きさ
imgs = concat_tile([[img, img_sobelx], [img_sobely, img_gradient]])
cv.imshow("img", imgs)
cv.imwrite("output.jpg", imgs)
if cv.waitKey(0) & 0xFF == ord('q'):
cv.destroyAllWindows()実行結果

左上が元画像、右上が横方向エッジ抽出、左下が縦方向のエッジ抽出、右下が勾配の大きさになります。
花の輪郭が抽出されているのが分かりますよね。
プログラム解説
サンプルプログラムを解説していきましょう。
ソーベルフィルタ適用は、cv.Sobel()関数を呼び出します。
cv.Sobel(img, cv.CV_64F, 1, 0, ksize=3)第1引数に読み込む画像、第2引数は、出力画像のビット深度を指定します。第3,4引数はx,yに関する微分の次数です。(1, 0)でx方向、(0, 1)でy方向のエッジが抽出できます。ksizeはフィルタ係数の大きさです。今回は3×3のフィルタサイズを指定しました。
ソーベルフィルタは微分値をとるため、負の値にもなります。しかし、負の値が含まれていると画像表示することが出来ません。そこで、cv.convertScaleAbs()関数を呼び出して絶対値にします。
cv.convertScaleAbs(img)縦方向と横方向のエッジを合成するには、cv.addWeighted()関数を呼び出します。
cv.addWeighted(src1, alpha1, src2, beta, gamma)出力結果は、\(\alpha\cdot src1 + \beta \cdot src2 + \gamma\)となります。
まとめ
今回は、ノイズを除去しつつエッジ抽出するソーベルフィルタについて解説しました。
- 微分によってエッジ検出する
- ソーベルフィルタとは、中央差分したのち、中央に重み付けした平滑化を行ったフィルタ
- OpenCVのcv.Sobel()関数によって、ソーベルフィルタを適用できる
これで、物体のエッジを抽出するプログラムが簡単に作れますね。
この記事が画像処理を学ぶ皆さんのためになれば幸いです。
独学が大変な方は、書籍やスクールを活用するのも手です。私も活用しているものを載せておきますので参考にして下さい。
最後までお読み頂きありがとうございました!