今回は、OpenCVを使って画像を平行移動・回転する方法について解説していきます。
画像の平行移動・回転は、アフィン変換という知識が必要です。
まず、アフィン変換について解説します。そして、OpenCVを使った画像処理プログラムを解説していきます。
アフィン変換とは
平面座標系のアフィン変換は3×3の行列を使って次式で表現できます。
$$ \left( \begin{array}{ccc} x’ \\ y’ \\ 1 \end{array} \right) = \left( \begin{array}{ccc} a & b & t_{x} \\ c & d & t_{y} \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \\ 1 \end{array} \right) $$
3行目って左辺が「1」、右辺も「1」でムダじゃない?
3行目は、実際の座標に加えて、仮想的な座標を付け加えています。このような座標系を同次座標系と呼びます。同次座標系による表現は、平行移動を行う上で重要となります。
平行移動
まず、アフィン変換を使って平行移動する方法を説明します。
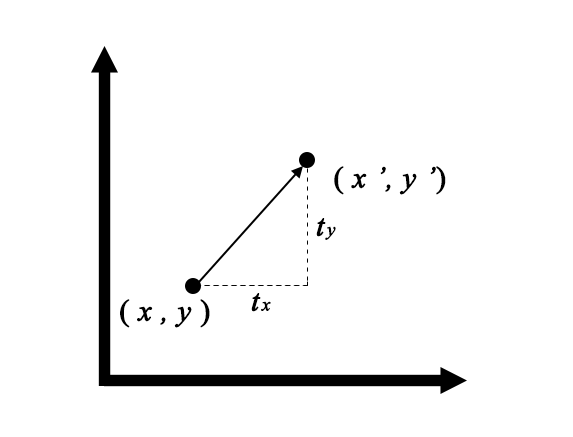
座標\((x,y)\)から\(x\)方向に\(t_{x}\)、\(y\)方向に\(t_{y}\)平行移動するとします。移動先の座標を\((x’,y’)\)としました。座標\((x’,y’)\)は、次の式で表せますね。
$$ \left( \begin{array}{ccc} x’ \\ y’ \end{array} \right) = \left( \begin{array}{ccc} x \\ y \end{array} \right) + \left( \begin{array}{ccc} t_{x} \\ t_{y} \end{array} \right) $$これを同次座標系で表現すると次の式で整理できます。
$$ \left( \begin{array}{ccc} x’ \\ y’ \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \\ 1 \end{array} \right) $$このように平行移動は、アフィン変換の3×3行列 \(a,b,c,d\)に\(a=d=1\)、\(b=c=0\)を代入すればよいことが分かります。
回転
次にアフィン変換を使って回転する方法の説明です。
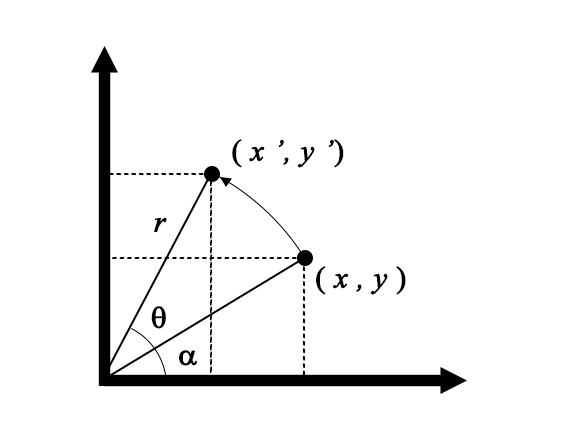
座標\((x,y)\)を原点中心に\(\theta\)角回転するとします。ここでも移動先の座標を\((x’,y’)\)としました。座標\((x’,y’)\)は次の式で表すことが出来ます。
$$ \left( \begin{array}{ccc} x’ \\ y’ \end{array} \right) = \left( \begin{array}{ccc} r \cos (\theta + \alpha) \\ r \sin (\theta + \alpha) \end{array} \right) $$ここで三角関数の加法定理を使うと
$$ \left( \begin{array}{ccc} x’ \\ y’ \end{array} \right) = \left( \begin{array}{ccc} r \cos \theta \cos \alpha – r \sin \theta \sin \alpha \\ r \sin \theta \sin \alpha + r \cos \theta \cos \alpha \end{array} \right) $$座標\((x,y)\)は
$$ \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} r \cos \alpha \\ r \sin \alpha \end{array} \right) $$ですので、座標\((x’,y’)\)は次式となります。
$$ \left( \begin{array}{ccc} x’ \\ y’ \end{array} \right) = \left( \begin{array}{ccc} x \cos \theta – y \sin \theta \\ x \sin \theta + y \cos \theta \end{array} \right) $$式を整理すると
$$ \left( \begin{array}{ccc} x’ \\ y’ \end{array} \right) = \left( \begin{array}{ccc} \cos \theta & – \sin \theta \\ \sin \theta & \cos \theta \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right) $$最後に、同次座標系で表現すると次式になります。
$$ \left( \begin{array}{ccc} x’ \\ y’ \\ 1 \end{array} \right) = \left( \begin{array}{ccc} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \\ 1 \end{array} \right) $$回転は、アフィン変換の3×3行列\(a,b,c,d\)に\(a=\cos\theta\)、\(b=-\sin\theta\)、\(c=\sin\theta\)、\(d=\cos\theta\)、\(t_{x}=0\)、\(t_{y}=0\)を代入すればよいことが分かります。
このように平行移動、回転はアフィン変換で実現できます。
OpenCVで画像の平行移動・回転
アフィン変換について理解できたと思いますので、本題のOpenCVで画像を平行移動・回転していきましょう!
今回は▼の画像を平行移動・回転します。画像は何でもよいですよ。

平行移動のプログラム
画像を平行移動するサンプルプログラムです。
import cv2 as cv
import numpy as np
#画像データの読み込み
img = cv.imread("sample.jpg")
height, width = img.shape[:2]
tx, ty = 100, 100
#アフィン変換: 平行移動
mv_mat = np.float32([[1, 0, tx],[0, 1, ty]])
afin_img = cv.warpAffine(img, mv_mat, (width, height))
cv.imshow("img", afin_img)
if cv.waitKey(0) & 0xFF == ord('q'):
cv.destroyAllWindows()水平方向に100、垂直方向に100移動させるため、\(t_{x}=100\)、\(t_{y}=100\)としました。アフィン変換の3×3行列 「mv_mat」を作成します。OpenCVでは、画像をアフィン変換するためのwarpAffine関数が用意されていますので、第1引数に移動対象の画像、第2引数にアフィン変換の行列、第3引数に出力画像サイズを指定しましょう。
出力結果が▼となります。

回転のプログラム
画像を回転するサンプルプログラムです。
import cv2 as cv
import numpy as np
#画像データの読み込み
img = cv.imread("sample.jpg")
height, width = img.shape[:2]
#アフィン変換: 回転
rot_mat = cv.getRotationMatrix2D((width/2, height/2), 45, 1)
afin_img = cv.warpAffine(img, rot_mat, (width, height))
cv.imshow("img", afin_img)
if cv.waitKey(0) & 0xFF == ord('q'):
cv.destroyAllWindows()前章で解説した回転のアフィン変換は、原点を中心に行われます。任意の点を中心に回転したい場合は、平行移動→回転→平行移動を繰り返す必要があります。OpenCVは、この処理を一括で行ってくれる関数があります。それがgetRotationMatrix2D関数です。第1引数に回転中心の座標、第2引数に角度、第3引数に拡大率を指定します。getRotationMatrix2D関数を実行するとアフィン変換の行列が戻り値として返ってきます。
出力結果が▼となります。

画像の中央点を中心に画像が回転されました。
まとめ
今回は、OpenCVを使って画像を平行移動・回転する方法について解説しました。
- 画像を平行移動・回転するためのアフィン変換について解説
- OpenCVで画像を平行移動・回転するプログラムを解説
画像処理ソフトがどうやって画像を平行移動・回転しているか理解出来たのではないかと思います。
今回の記事が皆さんのPython学習に役立つなら幸いです。
Python独学が大変な方は、書籍やスクールを活用するのも手です。